Unit 1, Day 7: Similar Triangles

Objective: Learn about similar triangles.

Two triangles are similar if the only distance is size or it is flipped or turned.

All of these triangles are similar. You can see this because of the same angles and that it is just different sizes.

How to tell if two triangles are similar.

If the two triangles have to same angles. 

If the corresponding sides have the same ratio.

In similar triangles, the sides facing the equal angles are always in the same ratio.

For example: 

Triangles R and S are similar. The equal angles are marked with the same numbers of arcs.

What are the corresponding lengths?

• The lengths 7 and a are corresponding (they face the angle marked with one arc)
• The lengths 8 and 6.4 are corresponding (they face the angle marked with two arcs)
• The lengths 6 and b are corresponding (they face the angle marked with three arcs)

Calculating the Lengths of Corresponding Sides

It may be possible to calculate lengths we don't know yet. We need to:

• Step 1: Find the ratio of corresponding sides in pairs of similar triangles.
• Step 2: Use that ratio to find the unknown lengths.

Example: Find lengths a and b of Triangle S above.

Step 1: Find the ratio

We know all the sides in Triangle R, and 
We know the side 6.4 in Triangle S

The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle R.

So we can match 6.4 with 8, and so the ratio of sides in triangle S to triangle R is:

6.4 to 8

Now we know that the lengths of sides in triangle S are all 6.4/8 times the lengths of sides in triangle R.

Step 2: Use the ratio

a faces the angle with one arc as does the side of length 7 in triangle R.

a = (6.4/8) × 7 = 5.6

b faces the angle with three arcs as does the side of length 6 in triangle R.

b = (6.4/8) × 6 = 4.8

Questions:

1.) A research team wishes to determine the altitude of a mountain as follows: They use a light source at L, mounted on a structure of height 2 meters, to shine a beam of light through the top of a pole P' through the top of the mountain M'. The height of the pole is 20 meters. The distance between the altitude of the mountain and the pole is 1000 meters. The distance between the pole and the laser is 10 meters. We assume that the light source mount, the pole and the altitude of the mountain are in the same plane. Find the altitude h of the mountain. 

2.) Show that the two triangles given beside are similar and calculate the lengths of sides PQand PR. 

3.) In the triangle ABC shown below, A'C' is parallel to AC. Find the length y of BC' and the length x of A'A.

Answers: 

1.) We first draw a horizontal line LM. PP' and MM' are vertical to the ground and therefore parallel to each other. Since PP' and MM' are parallel, the triangles LPP' and LMM' are similar. Hence the proportionality of the sides gives: 

1010 / 10 = (h - 2) / 18 

Solve for h to obtain 

h = 1820 meters.

2.) ∠A = ∠P and ∠B = ∠Q, ∠C = ∠R(because ∠C = 180 - ∠A - ∠B and ∠R = 180 - ∠P - ∠Q)

Therefore, the two triangles ΔABC and ΔPQR are similar.

3.) BA is a transversal that intersects the two parallel lines A'C' and AC, hence the corresponding angles BA'C' and BAC are congruent. BC is also a transversal to the two parallel lines A'C' and AC and therefore angles BC'A' and BCA are congruent. These two triangles have two congruent angles are therefore similar and the lengths of their sides are proportional. Let us separate the two triangles as shown below. 

• 
  
  
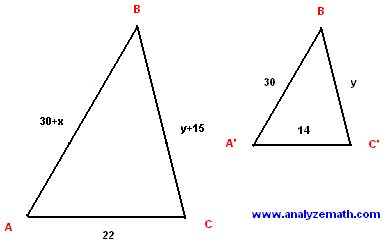
• We now use the proportionality of the lengths of the side to write equations that help in solving for x and y.
  
  (30 + x) / 30 = 22 / 14 = (y + 15) / y
  
• An equation in x may be written as follows.
  
  (30 + x) / 30 = 22 / 14
  
• Solve the above for x.
  
  420 + 14 x = 660
  
  x = 17.1 (rounded to one decimal place).
  
• An equation in y may be written as follows.
  
  22 / 14 = (y + 15) / y
  
• Solve the above for y to obtain. 
  
  y = 26.25